선형 변환(Linear Transformation)

vector function $T$ 에 대하여, T의 정의역에 속하는 모든 $\vec{u},\vec{v}$에 대해

$$T(c\vec{u}+d\vec{v})=cT(\vec{u})+dT(\vec{v})$$

를 만족시키는 function $T$를 Linear Transformation이라고 한다. ($c,d$는 스칼라 값)

1. 변환 후에도 원점의 위치가 변하지 않고,
2. 변환 후에 격자들이 직선을 유지하며,
3. 격자 간의 간격이 균등하게 되는 변환이 선형 변환의 필요조건이다.

선형 변환은 n차원의 벡터를 m차원의 벡터로 변환 시킬 수 있으며, 행렬과 입력값 벡터로 이루어지는 함수로 항상 표현된다.

$A$는 n x m의 행렬이며, ${\mathbb{R}}^m$ 차원의 벡터로 Linear transformation 한다.

Vector $\vec{m}$이 가리키는 점은 동일하지만, 이를 바라보는 축(즉, $A$의 Matrix Space)가 바뀌는 것으로 이해할 수 있다.

Martrix of Linear transformation

---

$T:{\mathbb{R}}^n\to {\mathbb{R}}^m$ 에 대해 ${\mathbb{R}}^{n\times n}$에 속하는 basis vector $\overrightarrow{e_n}$ 로 이루어진 행렬이 된다. 이를 Standard Matrix라고 한다.

Affine layer

---

fully-connected layer는, 항상 bias term을 가지게 된다. 이를 Affine Layer라고 한다.

입력층의 각 노드들로 이루어진 column vector에 대해 Linear Transformation 함수(Activation Function)을 이용해 weights를 조정해가며 계산한다. 그리고, bias vector를 더하게 된다.

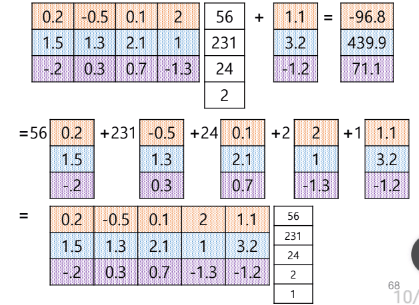
입력층의 각 노드들을 합쳐 column vector로 나타낼 때, bias term을 포함하는 column vector(${\mathbb{R}}^{n+1}$)로 바꾸어 나타내게 된다. 이를 위하여, 입력층에서 bias vector는 A행렬에 대해 추가되고, 그 벡터 부분은 입력 벡터의 새로 추가된, 1과 곱해지게 하여 새로운 Linear transformation을 만든다.